第5章 栈与队列

栈与队列是在程序设计中被广泛使用的两种重要的线性数据结构，它们都是在一个特定范围的存储单元中存储的数据，这些数据都可以重新被取出使用，与线性表相比，它们的插入和删除操作受到更多的约束和限定，故又称为限定性的线性表结构。两者不同的是，栈就像一个很窄的桶，先存进去的数据只能最后被取出来，是LIFO（Last In First Out，后进先出），它将进出顺序逆序，即先进后出，后进先出，栈结构如下图所示。

队列像日常排队买东西的人的“队列”，先排队的人先买，后排队的人后买，是FIFO （First In First Out，先进先出）的，它保持进出顺序一致，即先进先出，后进后出，队列结构下图所示。

需要注意的是，有时在数据结构中还有可能出现按照大小排队或按照一定条件排队的数据队列，这时的队列属于特殊队列，就不一定按照“先进先出”的原则读取数据了。

5.1 如何实现栈

难度系数：★★★☆☆

被考查系数：★★★★☆

题目描述：

实现一个栈的数据结构，使其具有以下方法：压栈、弹栈、取栈顶元素、判断栈是否为空以及获取栈中元素个数。

分析与解答：

栈的实现有两种方法，分别是采用数组来实现和采用链表来实现。下面会详细介绍这两种方法。

方法一：数组实现

在采用PHP数组来实现栈的时候，可以先创建一个空数组作为栈，在后期使用过程中每当向数组压入一个元素，数组的容量是可以自动扩容的。实现思路如下图所示。

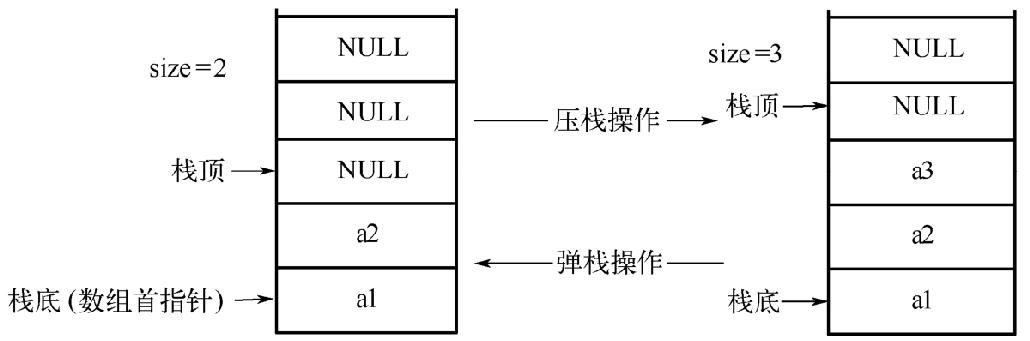
从上图中可以看出，可以把数组的首地址当作栈底，同时记录栈中元素的个数size，根据栈底指针和size就可以计算出栈顶的地址了。假设数组首地址为Arr，压栈的操作其实是把待压栈的元素放到数组Arr[size]中；同理，弹栈操作其实是取数组Arr[size-1]元素，然后用unset（）函数删除该键值。根据这个原理可以非常容易实现入栈或出栈。

实现代码如下：

程序的运行结果为

方法二：链表实现

在创建链表的时候经常采用一种从头结点插入新结点的方法，可以采用这种方法来实现栈，最好使用带头结点的链表，这样可以保证对每个结点的操作都是相同的，实现思路如下图所示。

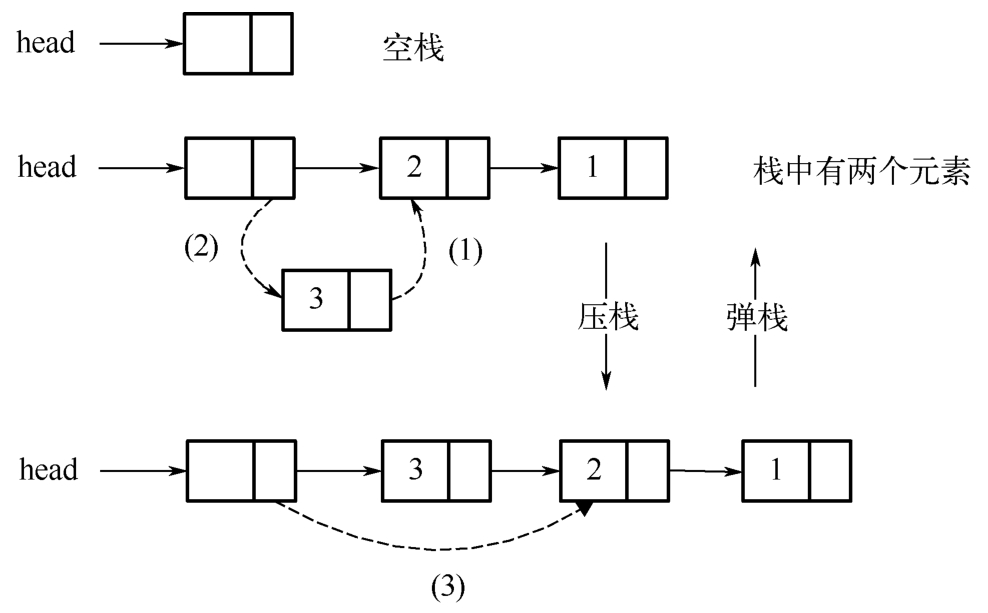
在上图中，在进行压栈操作时，首先需要创建新的结点，把待压栈的元素放到新结点的数据域中，然后只需要（1）和（2）两步就实现了压栈操作（把新结点加到了链表首部）。同理，在弹栈的时候，只需要进行步骤（3）的操作就可以删除链表的第一个元素，从而实现弹栈操作（被删除的结点所占的存储空间需要被释放）。实现代码如下：

程序的运行结果为

两种方法的对比：

采用数组实现栈的优点：一个元素值占用一个存储空间，数组可以动态的随元素进行扩容。

采用链表实现栈的优点：使用灵活方便，只有在需要的时候才会申请空间。它的缺点：除了要存储元素外，还需要额外的存储空间存储指针信息。

5.2 如何实现队列

难度系数：★★★☆☆

被考查系数：★★★★☆

题目描述：

实现一个队列的数据结构，使其具有入队列、出队列、查看队列首尾元素、查看队列大小等功能。

分析与解答：

与实现栈的方法类似，队列的实现也有两种方法，分别为采用数组来实现和采用链表来实现。下面分别详细介绍这两种方法。

方法一：数组实现

下图给出了一种最简单的实现方式，用front来记录队列首元素的位置，用rear来记录队列尾元素往后一个位置。入队列的时候只需要将待入队列的元素放到数组下标为rear的位置，同时执行rear++，出队列的时候只需要执行front++即可。

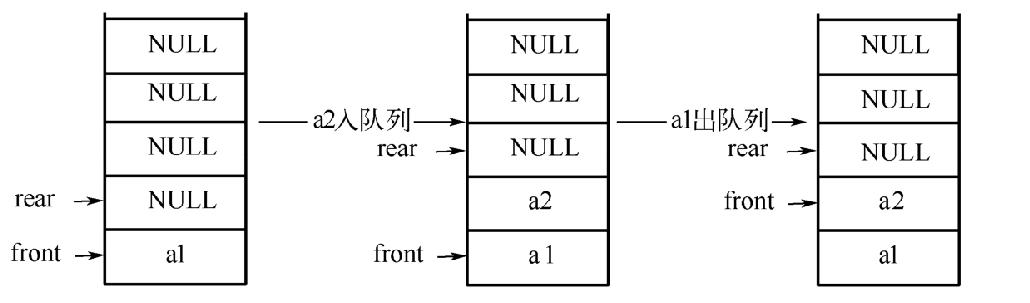
以向队列数组存入元素1，2为例，实现代码如下：

程序的运行结果为

方法二：链表实现

采用链表实现队列的方法与实现栈的方法类似，分别用两个指针指向队列的首元素与尾元素，如下图所示。用pHead来指向队列的首元素，用pEnd来指向队列的尾元素。

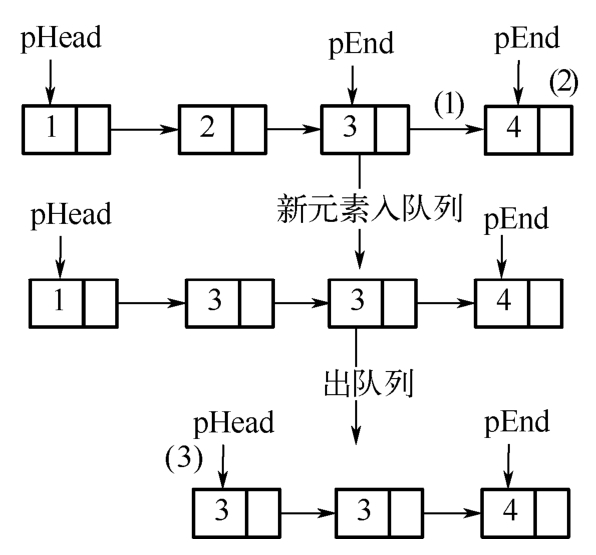
在上图中，刚开始队列中只有元素1、2和3，当新元素4要进队列的时候，只需要上图中（1）和（2）两步，就可以把新结点连接到链表的尾部，同时修改pEnd指针指向新增加的结点。出队列的时候只需要（3）这一步，改变pHead指针使其指向pHead→next，此外也需要考虑结点所占空间释放的问题。在入队列与出队列的操作中也需要考虑队列为空的时候的特殊操作，以向链表添加数据1，2为例，实现代码如下：

程序的运行结果为

此外，也可以用循环链表来实现队列，这样只需要一个指向链表最后一个元素的指针即可，因为通过指向链表尾元素可以非常容易地找到链表的首结点。

算法性能分析：

这两种方法压栈与弹栈的时间复杂度都为O（1）。

5.3 如何翻转栈的所有元素

难度系数：★★★★☆

被考查系数：★★★★☆

题目描述：

翻转（也叫颠倒）栈的所有元素，如输入栈[1, 2, 3, 4, 5]。其中，1处在栈顶，翻转之后的栈为[5, 4, 3, 2, 1]， 5处在栈顶。

分析与解答：

最容易想到的办法是，申请一个额外的队列，先把栈中的元素依次出栈放到队列里，然后把队列里的元素按照出队列顺序入栈，这样就可以实现栈的翻转，这种方法的缺点是，需要申请额外的空间存储队列，因此，空间复杂度较高。下面介绍一种空间复杂度较低的递归的方法。

递归程序有两个关键因素需要注意：递归定义和递归终止条件。经过分析后，很容易得到该问题的递归定义和递归终止条件。递归定义：将当前栈的最底元素移到栈顶，其他元素顺次下移一位，然后对不包含栈顶元素的子栈进行同样的操作。终止条件：递归下去，直到栈为空。递归的调用过程如下图所示。

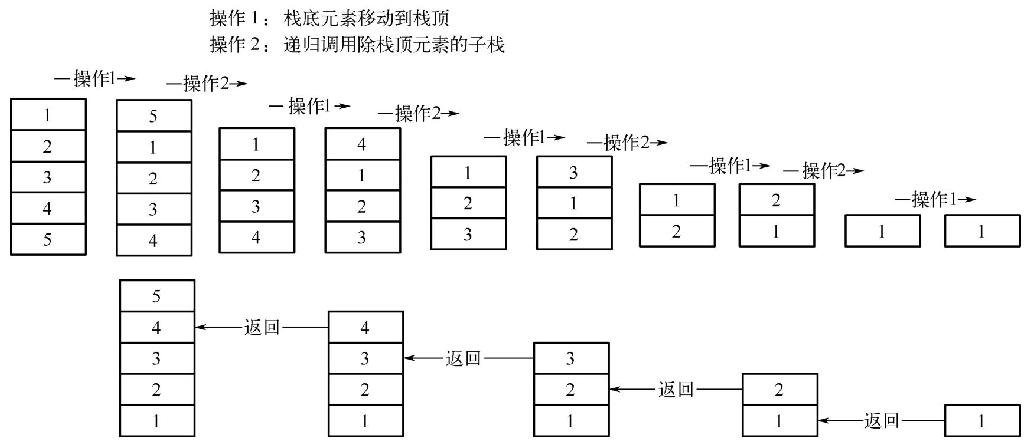
在上图中，对于栈（1, 2, 3, 4, 5），进行翻转的操作：首先把栈底元素移动到栈顶得到栈（5, 1, 2, 3, 4），然后对不包含栈顶元素的子栈进行递归调用（对子栈元素进行翻转），子栈（1, 2, 3, 4）翻转的结果为（4, 3, 2, 1），因此，最终得到翻转后的栈为（5, 4, 3, 2, 1）。

此外，由于栈的后进先出的特点，使得只能取栈顶的元素，因此，要把栈底的元素移动到栈顶也需要递归调用才能完成。主要思路：把不包含该栈顶元素的子栈的栈底的元素移动到子栈的栈顶，然后把栈顶的元素与子栈栈顶的元素（其实就是与栈顶相邻的元素）进行交换。

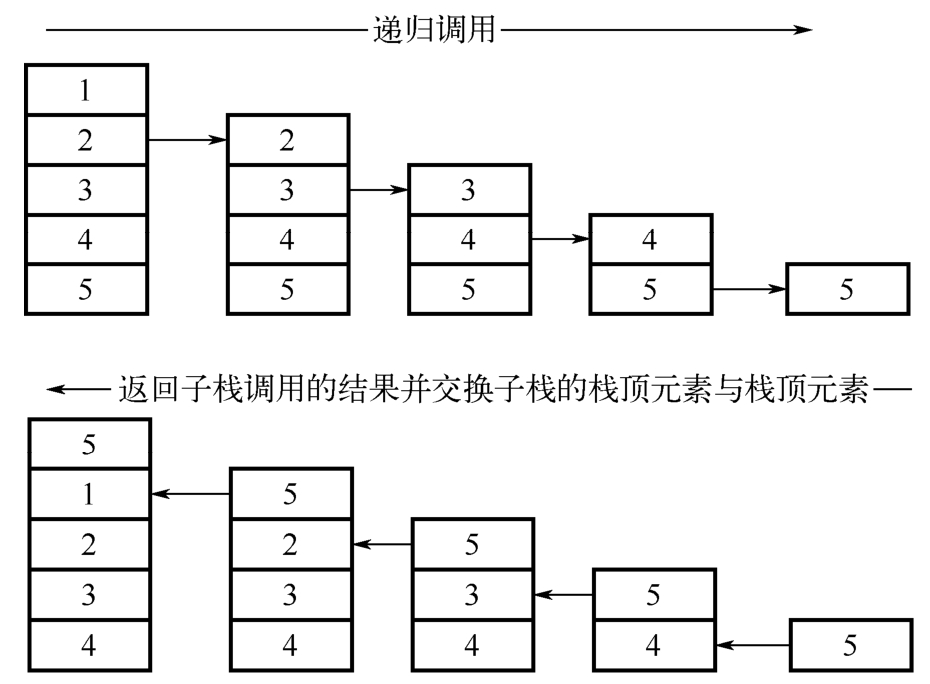
为了容易理解递归调用，可以认为在进行递归调用时，子栈已经实现了把栈底元素移动到了栈顶。在上图中为了把栈（1, 2, 3, 4, 5）的栈底元素5移动到栈顶，首先对子栈（2, 3, 4, 5），进行递归调用，调用的结果为（5, 2, 3, 4），然后对子栈顶元素5，与栈顶元素1进行交换得到栈（5, 1, 2, 3, 4），实现了把栈底元素移动到了栈顶。

实现代码如下：

程序的运行结果为

算法性能分析：

把栈底元素移动到栈顶操作的时间复杂度为O（n），在翻转操作中对每个子栈都进行了栈底元素移动到栈顶的操作，因此，翻转算法的时间复杂度为O（n2）。

引申：如何给栈排序。

分析与解答：

很容易通过对上述方法进行修改得到栈的排序算法。主要思路：首先对不包含栈顶元素的子栈进行排序，如果栈顶元素大于子栈的栈顶元素，则交换这两个元素。因此，在上述方法中，只需要在交换栈顶元素与子栈顶元素时增加一个条件判断即可实现栈的排序。

实现代码如下：

程序的运行结果为

算法性能分析：

算法的时间复杂度为O（n2）。

5.4 如何根据入栈序列判断可能的出栈序列

难度系数：★★★☆☆

被考查系数：★★★★★

题目描述：

输入两个整数序列，其中一个序列表示栈的push（入）顺序，判断另一个序列有没有可能是对应的pop（出）顺序。

分析与解答：

假如输入的push 序列是1、2、3、4、5，那么3、2、5、4、1就有可能是一个pop 序列，但5、3、4、1、2就不可能是它的一个pop 序列。

主要思路：使用一个栈来模拟入栈顺序，具体步骤如下：

1）把push序列依次入栈，直到栈顶元素等于pop序列的第一个元素，然后栈顶元素出栈，pop序列移动到第二个元素。

2）如果栈顶继续等于pop序列的元素，则继续出栈并把pop元素后移；否则对push序列继续入栈。

3）如果push序列已经全部入栈，但是pop序列未全部遍历，而且栈顶元素不等于当前pop元素，那么这个序列不是一个可能的出栈序列。如果栈为空，而且pop序列也全部被遍历过，则说明这是一个可能的pop序列。下图给出一个合理的pop序列的判断过程。

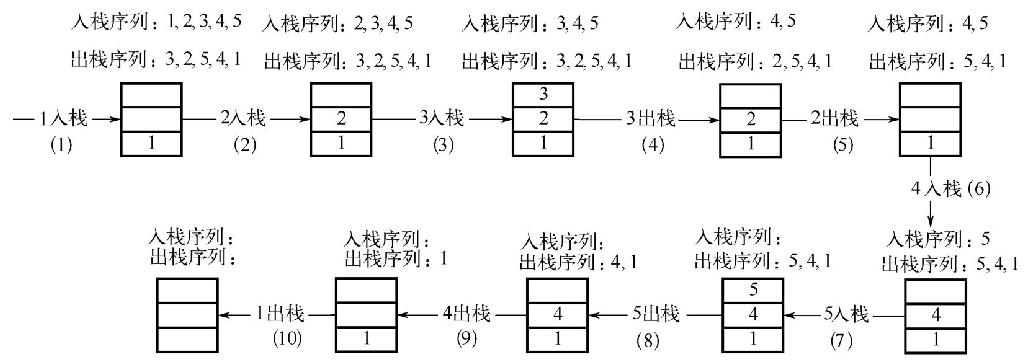
在上图中，（1）～（3）三步，由于栈顶元素不等于pop序列第一个元素3，因此，1, 2, 3依次入栈，当3入栈后，栈顶元素等于pop序列的第一个元素3。因此，第（4）步执行3出栈，接下来指向第二个pop序列2，且栈顶元素等于pop序列的当前元素。第（5）步执行2出栈；接着由于栈顶元素4不等于当前pop序列5。因此接下来（6）和（7）两步分别执行4和5入栈；接着由于栈顶元素5等于pop序列的当前值，第（8）步执行5出栈，接下来（9）和（10）两步栈顶元素都等于当前pop 序列的元素。因此，都执行出栈操作。最后由于栈为空，同时pop序列都完成了遍历，因此，（3, 2, 5, 4, 1）是一个合理的出栈序列。

实现代码如下：

程序的运行结果为

算法性能分析：

这个算法在处理一个合理的pop序列的时候需要操作的次数最多，即把push序列进行一次压栈和出栈操作，操作次数为2N。因此，时间复杂度为O（N）。此外，这个算法使用了额外的栈空间。因此，空间复杂度为O（N）。

5.5 如何用O（1）的时间复杂度求栈中最小元素

难度系数：★★★☆☆

被考查系数：★★★★☆

分析与解答：

由于栈具有后进先出的特点，因此push和pop只需要对栈顶元素进行操作。如果使用上述的实现方式，只能访问到栈顶的元素，无法得到栈中最小的元素。当然，可以用另外一个变量来记录栈底的位置，通过遍历栈中所有的元素找出最小值，但是这种方法的时间复杂度为O（n），那么如何才能用O（1）的时间复杂度求出栈中最小的元素呢？

在算法设计中，经常会采用空间来换取时间的方式来提高时间复杂度。也就是说，采用额外的存储空间来降低操作的时间复杂度。具体而言，在实现时使用两个栈结构，一个栈用来存储数据，另外一个栈用来存储栈的最小元素。实现思路如下：如果当前入栈的元素比原来栈中的最小值还小，则把这个值压入保存最小元素的栈中；在出栈时，如果当前出栈的元素恰好为当前栈中的最小值，保存最小值的栈顶元素也出栈，使得当前最小值变为入栈之前的那个最小值。为了简单起见，可以在栈中保存int类型。

通过数组作为栈，初始值为5，再向栈中压入6和2求最小元素，实现代码如下：

程序的运行结果为

算法性能分析：

这个算法申请了额外的一个栈空间来保存栈中最小的元素，从而实现了用O（1）的时间复杂度求栈中最小元素，但是付出的代价是空间复杂度为O（n）。

5.6 如何用两个栈模拟队列操作

难度系数：★★★☆☆

被考查系数：★★★★☆

分析与解答：

要求用两个栈来模拟队列，假设使用栈A与栈B模拟队列Q，其中A为插入栈，B为弹出栈。

再假设栈A和栈B都为空，可以认为栈A提供入队列的功能，栈B提供出队列的功能。

要入队列，入栈A即可，而出队列则需要分两种情况考虑：

1）如果栈B不为空，则直接弹出栈B的数据。

2）如果栈B为空，则依次弹出栈A的数据，放入栈B中，再弹出栈B的数据。

通过数组arr 1和arr 2两个栈为例，实现代码如下：

程序的运行结果为

算法性能分析：

这个算法入队操作的时间复杂度为O（1），出队操作的时间复杂度则依赖于入队与出队执行的频率。总体来讲，出队操作的时间复杂度为O（1），当然会有个别操作需要耗费更多的时间（因为需要从两个栈之间移动数据）。