第8章 基本数字运算
计算机软件技术与数学是不可切割的有机整体,很多企业在招聘求职者的时候,往往非常在意求职者的数学能力,站在企业的角度来看,编程语言是很简单的,只要熟悉一种语言,其他语言也很容易学会,而数学素养的高低却不然,需要长时间的学习与积累。数学能力直接决定了未来求职者的职业生涯的发展,所以面试官在考查求职者时,也比较喜欢出此类题目。
8.1 如何判断一个自然数是否是某个数的二次方
难度系数:★★★☆☆
被考查系数:★★★★☆
题目描述:
设计一个算法,判断给定的一个数n 是否是某个数的二次方,不能使用平方根运算。例如,16就满足条件,因为它是4的二次方;而15则不满足条件,因为不存在一个数其二次方值为15。
分析与解答:
方法一:直接计算法
由于不能使用平方根运算,因此最直接的方法就是计算二次方。主要思路:对1~n的每个数i,计算它的平方m,如果m<n,那么继续遍历下一个值(i+1),如果m=n,那么就说明n是m的二次方,如果m>n,那么就说明n不能表示成某个数的二次方。实现代码如下:


程序的运行结果为

算法性能分析
由于这个算法只需要从1遍历到n0.5就可以得出结果,因此算法的时间复杂度为O(n0.5)。
方法二:二分查找法
与方法一类似,这个方法的主要思路还是查找从1~n的数字中,是否存在一个数m,比m 的二次方为n。只不过在查找的过程中使用的是二分查找的方法。具体思路为:首先判断mid=(1+n)/2的二次方power与m的大小;如果power>m,那么就说明要在[1,mid-1]区间继续查找;否则在[mid+1,n]区间继续查找。
实现代码如下:


算法性能分析:
由于这个算法使用了二分查找的方法,因此时间复杂度为O(log2n),其中,n为数的大小。
方法三:减法运算法
通过对二次方数进行分析发现有如下规律:
(n+1)2=n2+2n+1=(n-1)2+(2×(n-1)+1)+2×n+1=…=1+(2×1+1)+(2×2+1)+…+(2×n+1)
通过上述公式可以发现,这些项构成了一个公差为2的等差数列的和。由此可以得到如下的解决方法:对n依次减1,3,5,7…,如果相减后的值大于0,则继续减下一项;如果相减后的值等于0,那么说明n是某个数的二次方;如果相减后的值小于0,那么说明n不是某个数的二次方。根据这个思路,实现代码如下:

算法性能分析:
这个算法的时间复杂度仍然为O(n0.5)。但由于方法一使用的是乘法操作,而这个算法采用的是减法操作,因此这种方法的执行效率比算法一更高。
8.2 如何判断一个数是否为2的n次方
难度系数:★★★★☆
被考查系数:★★★★★
分析与解答:
方法一:构造法
2的n次方可以表示为:20,21,22,…,2n,如果一个数是2的n次方,最直观的想法就是对1执行了移位操作(每次左移一位),即通过移位得到的值必定是2的n次方(针对n的所有取值构造出所有可能的值)。所以,要想判断一个数是否为2的n次方,只需要判断该数移位后的值是否与给定的数相等。以自然数8和9为例,实现代码如下:

程序的运行结果为

算法性能分析:
上述算法的时间复杂度为O(log2n)。
方法二:“与”操作法
那么是否存在效率更高的算法呢?通过对20,21,22,…,2n进行分析,发现这些数字的二进制形式分别为:1,10,100,…。从二进制的表示可以看出,如果一个数是2的n次方,那么这个数对应的二进制表示中有且只有一位是1,其余位都为0。因此,判断一个数是否为2的n次方可以转换为这个数对应的二进制表示中是否只有一位为1。如果一个数的二进制表示中只有一位是1,例如num=00010000,那么num-1的二进制表示为num-1=00001111。由于num与num-1二进制表示中每一位都不相同,因此num&(num-1)的运算结果为0。可以利用这种方法来判断一个数是否为2的n次方。实现代码如下:

算法性能分析:
这个方法的时间复杂度为O(1)。
8.3 如何不使用除法操作符实现两个正整数的除法
难度系数:★★★★☆
被考查系数:★★★☆☆
分析与解答:
方法一:减法
主要思路为:使被除数不断减去除数,直到相减的结果小于除数为止。此时,商就为相减的次数,余数为最后相减的差。例如,在计算14除以4时,首先计算14-4=10,由于10>4,继续做减法运算:10-4=6,6-4=2,此时2<4。由于总共进行了3次减法操作,最终相减的结果为2。因此,15除以4的商为3,余数为2。如果被除数比除数小,那么商就为0,余数为被除数。实现代码如下:

程序的运行结果为

算法性能分析:
这个方法循环的次数为m/n,因此算法的时间复杂度为O(m/n)。需要注意的是,这个方法也实现了不用%操作符也能实现%运算的目的。
方法二:移位法
方法一所采用的减法操作,还可以用等价的加法操作来实现。例如,在计算17除以4时,可以尝试4×1,4×2(即4+4),4×3(即4+4+4)依次进行计算,直到计算的结果大于14时就可以很容易求出商与余数。但是这种算法每次都递增4,效率较低。下面给出另外一种增加递增速度的方法:以2的指数进行递增(之所以取2的指数是因为该操作可以通过移位来实现,有更高的效率),计算4×1,4×2,4×4,4×8,由于4×8>17,所以结束指数递增,计算17-4×4,再进入下一次循环。实现代码如下:

算法性能分析:
由于这个算法采用指数级的增长方式不断逼近m/n,因此算法的时间复杂度为O(log2(m/n))。
引申一:如何不用加减乘除运算实现加法运算。
分析与解答:
由于不能使用加减乘除运算,因此只能使用位运算。首先通过分析十进制加法的规律来找出二进制加法的规律,从而把加法操作转换为二进制的操作来完成。
十进制的加法运算过程可以分为以下3个步骤:
1)各个位相加而不考虑进位,计算相加的结果sum。
2)只计算各个位相加时进位的值carry。
3)将sum与carry相加就可以得到这两个数相加的结果。
例如,15+29的计算方法为:sum=34(不考虑进位),carry=10(只计算进位),因此,15+29=sum+carry=34+10=44。
同理,二进制加法与十进制加法有着相似的原理,唯一不同的是,在二进制加法中,sum与carry的和可能还有进位,因此在二进制加法中会不停地执行sum+carry操作,直到没有进位为止。具体实现方法如下:
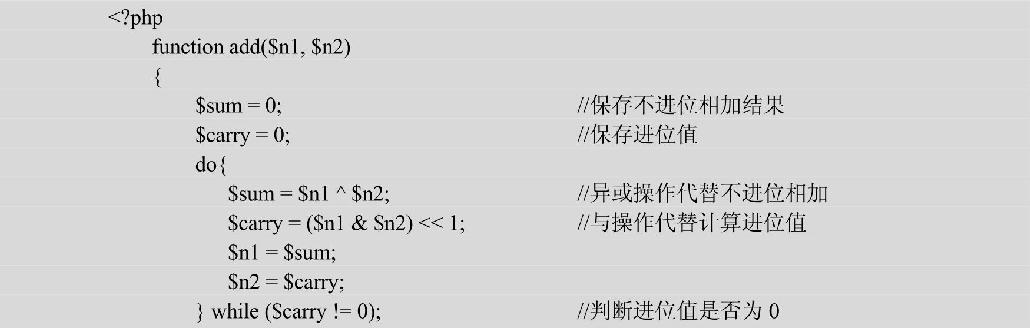
1)二进制各个位相加而不考虑进位。在不考虑进位的时候加法操作可以用异或操作代替。
2)计算进位,由于只有1+1才会产生进位,因此,进位的计算可以用“与”操作代替。进位的计算方法为:先做与运算,再把运算结果左移一位。
3)不断对1)、2)两步得到的结果相加,直到进位为0时为止。
实现代码如下:

程序的运行结果为

引申二:如何不用加减乘除运算实现减法运算。
分析与解答:
由于减去一个数等于加上这个数的相反数,即-n=~(n-1)=~n+1,因此a-b=a+(-b)=a+(~b)+1,可以利用上面已经实现的加法操作来实现减法操作。实现代码如下:


引申三:如何不用加减乘除运算实现乘法运算。
分析与解答:
以11×14为例介绍乘法运算的规律,11的二进制可以表示为1011,14的二进制可以表示为1110,二进制相乘的运算过程如下:
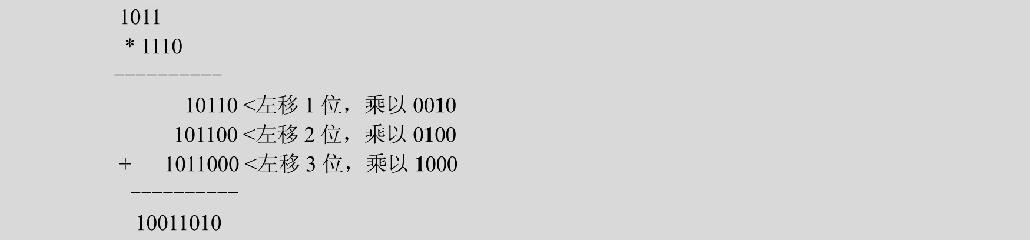
二进制数10011010的十进制表示为154=11×14。从这个例子可以看出,乘法运算可以转换为加法运算。计算a×b的主要思路为:①初始化运算结果为0,sum=0;②找到b对应二进制中最后一个1的位置i(位置编号从右到左依次为0, 1, 2, 3, …),并去掉这个1;③执行加法操作sum+=a<i;④循环执行①~③步,直到b对应的二进制数中没有更多的1为止。
从8.2节中可知,对n执行n&(n-1)操作可以去掉n的二进制数表示中的最后一位1,因此n&~(n-1)的结果为只保留n的二进制数中的最后一位1。因此,可以通过n&~(n-1)找出n 中最后一个1的位置,然后通过n&(n-1)去掉最后一个1。在上述的第②步中,首先执行lastBit=n&~(n-1),得到的值lastBit只包含n对应的二进制表示中最后一位1,要想确定1的位置,需要通过对1不断进行左移操作,直到移位的结果等于lastBit时移位的次数就是位置编号。在实现的时候,为了提高程序的运行效率,可以把1向左移动的位数(0~31)先计算好并保存起来。实现代码如下:

引申四:另外一种除法的实现方式。
分析与解答:
由于除法是乘法的逆运算,因此可以很容易地将除法运算转换为乘法运算。实现代码如下:


8.4 如何只使用++操作符实现加减乘除运算
难度系数:★★★☆☆
被考查系数:★★★☆☆
分析与解答:
本题要求只使用递增操作(++)来实现加减乘除运算,下面重点介绍该操作的计算过程:
1)加法操作。实现a+b的基本思路为对a执行b次++操作即可。
2)减法操作。实现a-b(a≥b)的基本思路为:不断对b执行++操作,直到等于a为止,在这个过程中记录执行++操作的次数。
3)乘法操作。实现a×b的基本思路为:利用已经实现的加法操作把a相加b次,就得到了a×b的值。
4)除法操作。实现a/b的基本思路为:利用乘法操作,使b不断乘以1,2,…,n,直到b×n>b时,就可以得到商为n-1。
以自然数2和-4为例,实现代码如下:



程序的运行结果为

此外,在实现加法操作的时候,如果a与b都是整数,那么就可以选择比较小的数进行循环,可以提高算法的性能。
8.5 如何根据已知随机数生成函数计算新的随机数
难度系数:★★★★☆
被考查系数:★★★★☆
题目描述:
已知随机数生成函数rand7()能产生的随机数是整数1~7的均匀分布,如何构造rand10()函数,使其产生的随机数是整数1~10的均匀分布。
分析与解答:
要保证rand10()产生的随机数是整数1~10的均匀分布,可以构造一个1~10×n的均匀分布的随机整数区间(n为任何正整数)。假设x是这个1~10×n区间上的一个随机数,那么x%10+1就是均匀分布在1~10区间上的整数。
根据题意,rand7()函数返回1~7的随机数,那么rand7()-1则得到一个离散整数集合,该集合为{0,1,2,3,4,5,6},该集合中每个整数的出现概率都为1/7。那么(rand7()-1)×7得到另一个离散整数集合A,该集合元素为7的整数倍,即A={0,7,14,21,28,35,42}。其中,每个整数的出现概率也都为1/7。而由于rand7()得到的集合B={1,2,3,4,5,6,7},其中每个整数出现的概率也为1/7。显然集合A与集合B中任何两个元素和组合相加得到的和可以与1~49之间的一个整数一一对应,即1~49之间的任何一个数,可以唯一地确定A和B中两个元素的一种组合方式,这个结论反过来也成立。由于集合A和集合B中元素可以看成是独立事件,根据独立事件的概率公式P(AB)=P(A)P(B),得到每个组合的概率是1/7×1/7=1/49。因此,(rand7()-1)×7+rand7()生成的整数均匀分布在1~49之间,而且每个数的概率都是1/49。
(rand7()-1)×7+rand7()可以构造出均匀分布在1~49的随机数,为了将49种组合映射为1~10之间的10种随机数,就需要进行截断,即将41~49这样的随机数剔除掉,得到的数1~40仍然是均匀分布在1~40的,这是因为每个数都可以看成一个独立事件。由1~40区间上的一个随机数x,可以通过计算x%10+1得到均匀分布在1~10区间上的整数。
实现代码如下:


程序运行后得到的结果是随机的,下面只列出了其中的一种显示情况。

8.6 如何判断1024!末尾有多少个0
难度系数:★★★★☆
被考查系数:★★★★☆
分析与解答:
方法一:暴力法
最简单的方法就是计算出1024!的值,然后判断末尾有多少个0。但是这种方法有两个非常大的缺点:第一,算法的效率非常低下;第二,当这个数字比较大的时候直接计算阶乘可能会导致数据溢出,从而导致计算结果出现偏差。因此,下面给出另外一种比较巧妙的方法。
方法二:因子法
5与任何一个偶数相乘都会增加末尾0的个数,由于偶数的个数肯定比5的个数多,因此1~1024所有数字中有5的因子的数字的个数决定了1024!末尾0的个数。因此,只需要统计因子5的个数即可。此外,5与偶数相乘会使末尾增加一个0,25(有两个因子5)与偶数相乘会使末尾增加两个0,125(有三个因子5)与偶数相乘会使末尾增加三个0,625(有四个因子5)与偶数相乘会使末尾增加四个0。对于本题而言:
1)是5的倍数的数有:a1=1024/5=204个。
2)是25的倍数的数有:a2=1024/25=40个(a1计算了25中的一个因子5)。
3)是125的倍数的数有:a3=1024/125=8个(a1、a2分别计算了125中的一个因子5)。
4)是625的倍数的数有:a4=1024/625=1个(a1、a2、a3分别计算了625中的一个因子5)。
所以,1024! 中总共有a1+a2+a3+a4=204+40+8+1=253个因子5。因此,末尾总共有253个0。实现代码如下:


程序的运行结果为

算法性能分析:
由于这个算法循环的次数为n/5,因此算法时间复杂度为O(n)。
引申:如何计算N!末尾有几个0?
分析与解答:
从以上的分析可以得出N!末尾0的个数为N/5+N/52+N/53+…+N/5m(5m<N且5(m+1)>N)。
8.7 如何按要求比较两个数的大小
难度系数:★★★☆☆
被考查系数:★★★★★
题目描述:
请定义一个函数,比较a、b两个数的大小,不能使用大于和小于两个比较运算符以及if条件语句。
分析与解答:
方法一:绝对值法
根据绝对值的性质可知,如果|a-b|=a-b,那么max(a,b)=a;否则max(a,b)=b,以自然数5和6为例,实现代码如下:

程序的运行结果为

方法二:二进制法
如果a>b,那么a-b的二进制最高位为0,与任何数的与操作的结果还是0;如果a-b为负数,那么a-b的二进制最高位为1,与0×80000000(最高位为1,其他位为0,假设a与b都占4个字节)执行“与”操作之后为结果为1。由此根据两个数的差的二进制最高位的值就可以比较两个数的大小,实现方法如下:

或
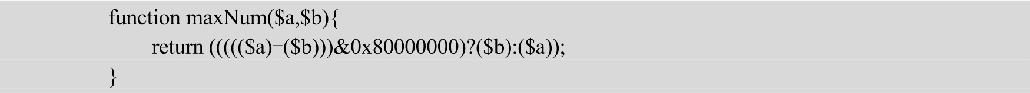
8.8 如何求有序数列的第1500个数的值
难度系数:★★★★☆
被考查系数:★★★☆☆
题目描述:
一个有序数列,序列中的每一个值都能够被2或者3或者5所整除,1是这个序列的第一个元素。求第1500个数的值是多少。
分析与解答:
方法一:蛮力法
最简单的方法就是用一个计数器来记录满足条件的整数的个数,然后从1开始遍历整数,如果当前遍历的数能被2或者3或者5整除,那么计数器的值加1,当计数器的值为1500时,当前遍历到的值就是所要求的值。实现代码如下:

程序的运行结果为

方法二:数字规律法
首先可以很容易得到2、3和5的最小公倍数为30。此外,1~30这个区间内满足条件的数有22个(2,3,4,5,6,8,9,10,12,14,15,16,18,20,21,22,24,25,26, 27,28,30)。由于最小公倍数为30,可以猜想,满足条件的数字是否具有周期性(周期为30)呢?通过计算可以发现,31~60这个区间内满足条件的数也恰好有22个(32,33,34, 35,36,38,39,40,42,44,45,46,48,50,51,52,54,55,56,57,58,60),从而发现这些满足条件的数具有周期性(周期为30)。由于1500/22=68,1500%68=4,从而可以得出第1500个数经过了68个周期,然后在第69个周期中取第四个满足条件的数(即1~30这个区间内满足条件的第4个数)。从而可以得出第1500个数为68×30+5=2045。实现代码如下:

算法性能分析:
方法二的时间复杂度为O(1)。此外,方法二使用了22个额外的存储空间。方法二的计算方法可以用来分析方法一的执行效率。从方法二的实现代码可以得出,方法一中循环执行的次数为(n/22)×30+a[n%22],其中,a[n%22]的取值范围为2~30,因此方法一的时间复杂度为O(n)。
8.9 如何求二进制数中1的个数
难度系数:★★★☆☆
被考查系数:★★★★☆
题目描述:
给定一个整数,输出这个整数的二进制表示中1的个数。例如,给定整数7,其二进制表示为111,因此输出结果为3。
分析与解答:
方法一:移位法
可以采用位操作来完成。具体思路如下:首先,判断这个数的最后一位是否为1,如果为1,则计数器加1。然后,通过右移丢弃掉最后一位,循环执行该操作直到这个数等于0为止。在判断二进制表示的最后一位是否为1时,可以采用“与”运算来达到这个目的。实现代码如下:


程序的运行结果为

算法性能分析:
这个算法的时间复杂度为O(n),其中,n代表二进制数的位数。
方法二:“与”操作法
给定一个数n,每进行一次n&(n-1)计算,其结果中都会少了一位1,而且是最后一位。例如,n=6,其对应的二进制表示为110;n-1=5,对应的二进制表示为101;n&(n-1)运算后的二进制表示为100,其效果就是去掉了110中最后一位1。可以通过不断地用n&(n-1)操作去掉n中最后一位1的方法求出n中1的个数。实现代码如下:

算法性能分析:
这个算法时间复杂度为O(m),其中m 为二进制数中1的个数。显然,当二进制数中1的个数比较少时,这个算法有更高的效率。
8.10 如何计算一个数的n次方
难度系数:★★★★☆
被考查系数:★★★★☆
题目描述:
给定一个数d和n,如何计算d的n次方?例如,d=2、n=3,d的n次方为23=8。
分析与解答:
方法一:蛮力法
可以把n的取值分为如下几种情况:
1)当n=0时,计算结果肯定为1。
2)当n=1时,计算结果肯定为d。
3)当n>0时,计算方法为:初始化计算结果result=1,然后对result执行n次乘以d的操作,得到的结果就是d的n次方;
4)当n<0时,计算方法为:初始化计算结果result=1,然后对result执行|n|次除以d的操作,得到的结果就是d的n次方;
以2的三次方为例,首先初始化result=1,接着对result 执行三次乘以2的操作:result=result×2=1×2=2,result=result×2=2×2=4,result=result×2=4×2=8,因此,2的三次方等于8。根据这个思路给出实现代码如下:

程序的运行结果为

算法性能分析:
这个算法时间复杂度为O(n),需要注意的是,当n非常大的时候,这种算法的效率是非常低下的。
方法二:递归法
由于方法一没有充分利用中间的计算结果,因此,算法效率还有很大的提升的余地。例如,在计算2的100次方时,假如已经计算出了2的50次方的值tmp=250,就没必要对tmp再乘以50次2,而可以直接利用tmp*tmp就得到了2100的值。通过这个特点可以用递归的方式实现n次方的计算,具体过程如下:
1)当n=0时,计算结果肯定为1。
2)当n=1时,计算结果肯定为d。
3)当n>0时,首先计算2n/2的值tmp;如果n为奇数,那么计算结果result=tmp*tmp*d;如果n为偶数,那么计算结果result=tmp*tmp。
4)当n<0时,首先计算2(|n/2|)的值tmp;如果n 为奇数,那么计算结果result=1/(tmp*tmp*d);如果n为偶数,那么计算结果result=1/(tmp*tmp)。
但需要注意,该方法不能计算出一个数的负n次方,要求n必须≥0。
实现代码如下:

算法性能分析:
这个算法的时间复杂度为O(log2n)。
8.11 如何在不能使用库函数的条件下计算正数n的算术平方根
难度系数:★★★☆☆
被考查系数:★★★★☆
题目描述:
给定一个数n,求出它的算术平方根,例如,16的算术平方根为4。要求不能使用库函数。
分析与解答:
正数n 的算术平方根可以通过计算一系列近似值来获得,每个近似值都比前一个更加接近准确值,直到找出满足精度要求的那个数为止。具体而言,可以找出第一个近似值是1,接下来的近似值则可以通过下面的公式来获得:ai+1=(ai+n/ai)/2。实现代码如下:

程序的运行结果为

8.12 如何不使用^操作实现异或运算
难度系数:★★★☆☆
被考查系数:★★★★☆
题目描述:
不使用“^”操作实现异或运算。
分析与解答:
最简单的方法是遍历两个整数的所有的位,如果两个数的某一位相等,那么结果中这一位的值就为0,否则结果中这一位的值就为1。以自然数3和5进行运算为例,实现代码如下:


程序的运行结果为

下面介绍另外一种更加简便的实现方法:x^y=(x|y)&(~x| ~y),其中x|y表示如果在x或y中的bit为1,那么结果的这一个bit的值也为1。显然这个结果包括三部分:这个位只有在x中为1,或只有在y中为1,或在x和y中都为1。要在这个基础上计算出异或的结果,显然要去掉第三种情况,也就是说,去掉在x和y中都为1的情况,而当一个bit在x和y中都为1时“~x| ~y”的值为0,因此 (x|y)&(~x| ~y)的值等于x^y。实现代码如下:

算法性能分析:
这个算法的时间复杂度为O(n)。
8.13 如何不使用循环输出1~100
难度系数:★★★☆☆
被考查系数:★★★★☆
题目描述:
实现一个函数,要求在不使用循环的前提下输出1~100。
分析与解答:
很多情况下,循环都可以使用递归来给出等价的实现,实现代码如下:

程序的运行结果为



 在线客服
在线客服
共有0条评论 网友评论
暂无评论,快来抢沙发吧!