【典型应用1】方程与不等式
(☆☆)【7.1.1】
已知a,b,c都是奇数,求证:方程ax2+bx+c=0没有整数解.
【解析】
设方程有整数解x,若x为奇数,则方程的左边ax2,bx,c都是奇数,则左边的ax2+bx+c是奇数,右边0为偶数,所以等式不成立.若方程的整数解x为偶数,那么ax2,bx都是偶数,又因为c为奇数,所以ax2+bx+c仍是奇数,等式依然不成立.所以方程的解既不可能是奇数,也不可能是偶数,所以方程ax2+bx+c=0没有整数解.
(☆☆)【7.1.2】
求证:当x2+bx+c2=0有两个不相等的非零实数根时,必有bc≠0.
【解析】
bc≠0的否定是bc=0,而bc=0有三种情况:①b=0,c=0;②b=0,c≠0;③b≠0,c=0.
证明如下:假设bc=0.
①若b=0,c=0,方程变为x2=0,那么x1=x2=0是方程x2+bx+c2=0的根.
②若b=0,c≠0,方程变为x2+c2=0,x2=-c2,又因为c≠0,所以x无解.
③若b≠0,c=0,方程变为x2+bx=0,方程的根为x1=0,x2=-b.
上述三种情况均与已知条件中“方程有两个不相等的非零实数根”矛盾.所以bc≠0.
【备注】
证明“不等于”往往比较困难,所以通过反证法将其转化为“等于”问题来证明.
(☆☆)【7.1.3】
已知0<a,b,c<1,求证:(1-a)b,(1-b)c,(1-c)a不可能同时大于 .
.
【解析】
假设(1-a)b,(1-b)c,(1-c)a同时大于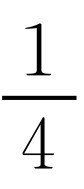 ,则
,则
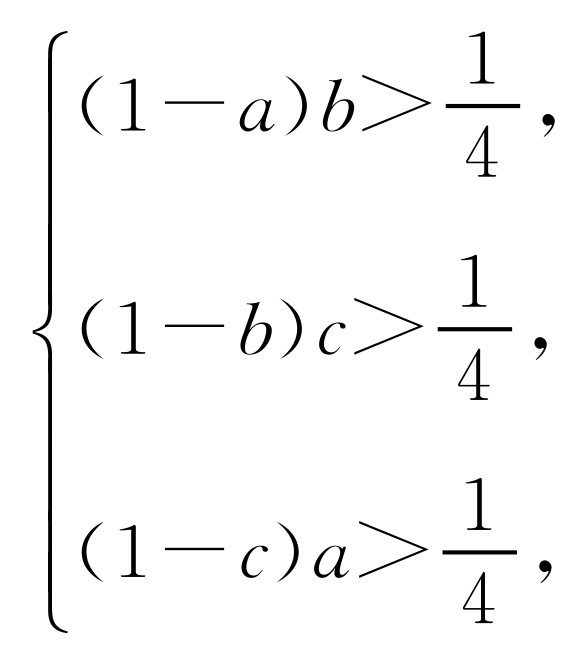 即
即 ,将三式相加
,将三式相加
得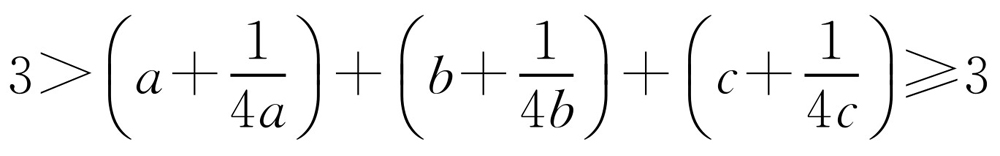 ,矛盾.所以(1-a)b,(1-b)c,(1-c)a不可能同时大于
,矛盾.所以(1-a)b,(1-b)c,(1-c)a不可能同时大于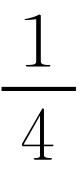 .
.
(☆☆☆)【7.1.4】
设实数a0,a1,a2,…,an-1,an满足:a0=an=0,a0-2a1+a2≥0,a1-2a2+a3≥0,…,an-2-2an-1+an≥0.求证:ai≤0(i=1,2,…,n).
【解析】
设ar是a0,a1,a2,…,an-1,an中的第一个正数,即a1≤0,a2≤0,…,ar-1≤0,ar>0
则ar-ar-1>0.由已知条件变形得ai+1-ai≥ai-ai-1(i=1,2,…,n-1).所以当i≥r时,ar-ar-1>0,ar+1-ar>0,…,an-an-1>0.所以0<ar<ar+1<…<an,与已知条件an=0矛盾.
(☆☆☆)【巩固练习1】
已知下列三个方程:x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根,求实数a的取值范围.





 在线客服
在线客服
共有0条评论 网友评论
正在狠努力加载,请稍候...