【典型应用1】化简求值
（☆☆）【27.1.1】
解方程：（2x2-3x+1）2=22x2-33x+1.
【解析】
令2x2-3x=a，原式为（a+1）2=11a+1，求解得出a的值，从而得到x的解可能是x=0，
或x=3.
【备注】
换元法在解代数方程中一般是为了降次，所以换元法常用于高次方程．
（☆☆）【27.1.2】
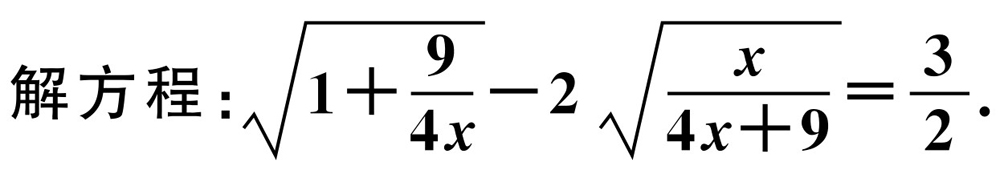
【解析】
令
，则
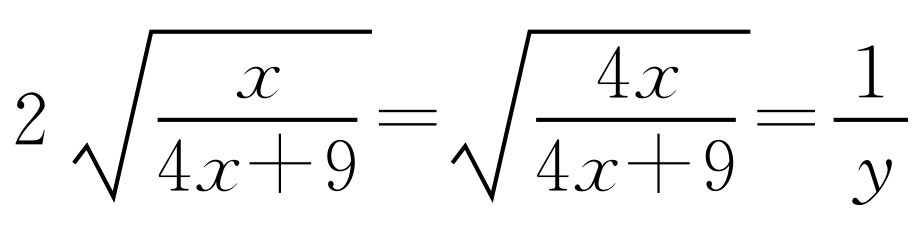.原式化为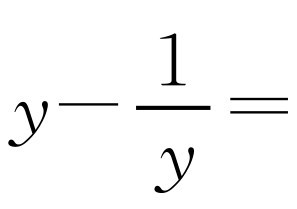
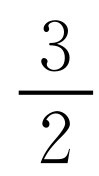，求解出y的值，从而得到
.
（☆☆）【27.1.3】
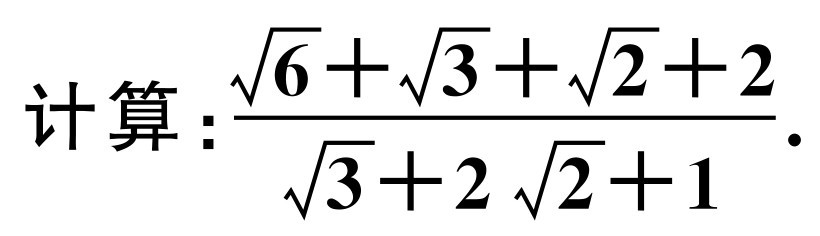
【解析】
，则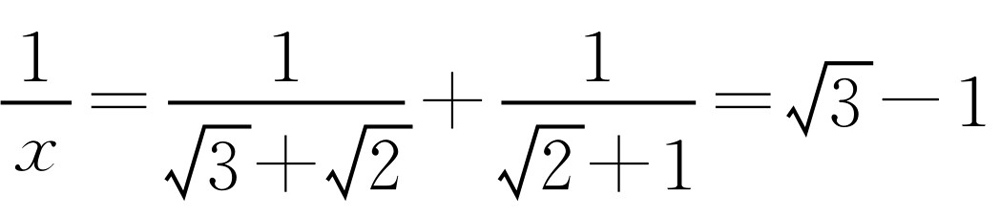
，故原式的值为
.
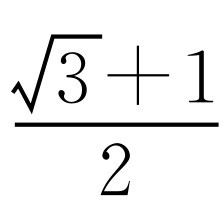【备注】
本题也可如此换元，令
，则
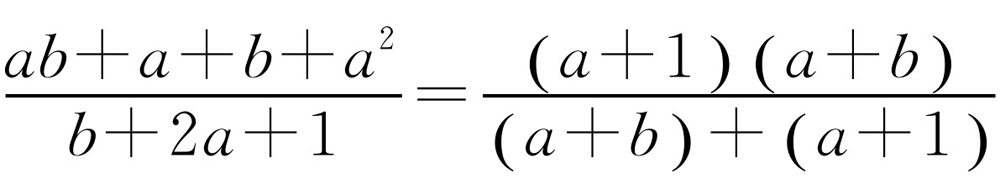更明显．
（☆☆☆）【27.1.4】
求不超过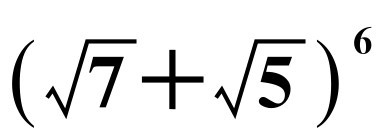
的最大整数．
【解析】
设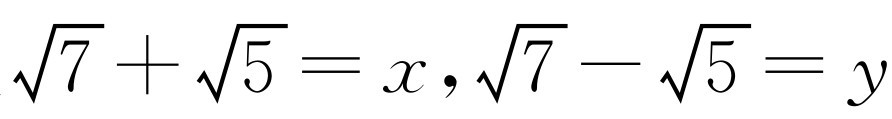
，则
，故x2+y2=（x+y）2-2xy=24，x6+y6=（x2+y2）3-3（xy）2（x2+y2）=13 536，
．因为
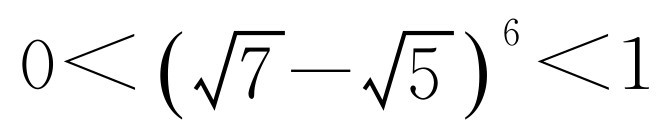，故不超过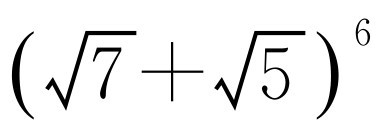
的最大整数为13 535.
（☆☆☆）【27.1.5】
已知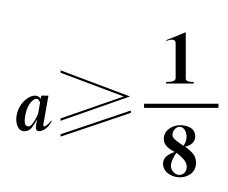
，化简求值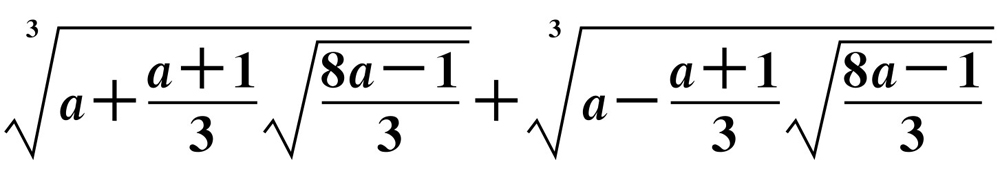
.
【解析】
令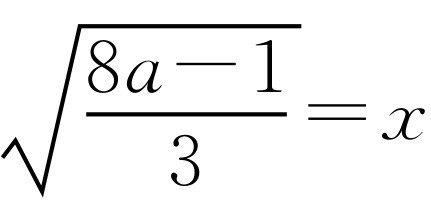
，则
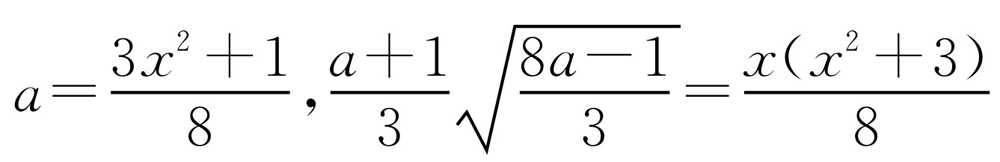，故
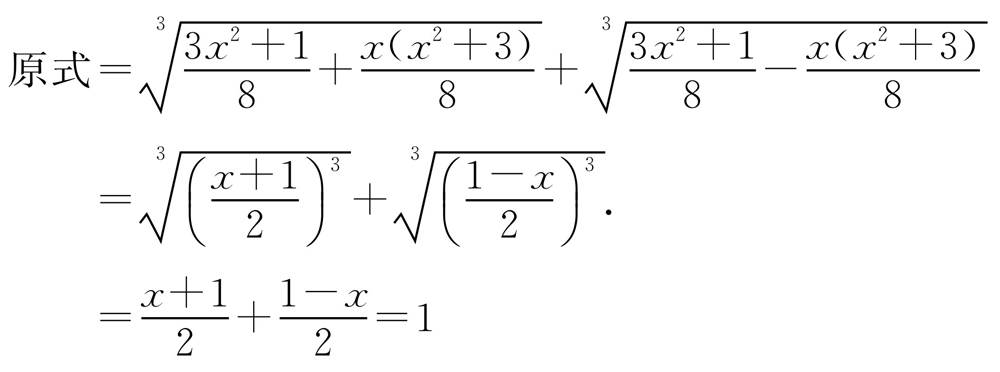
（☆☆☆）【巩固练习1】
化简：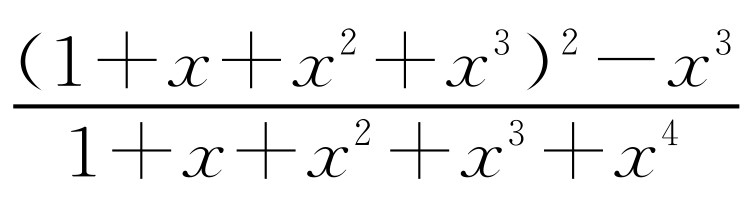
.
在线客服
共有条评论 网友评论