【典型应用3】证明相关
（☆☆）【27.3.1】
求证：（m+n）（m+n-2mn）+（mn-1）（mn+1）=（m+n-mn+1）×（m+n-mn-1）.
【解析】
令m+n=a，mn=b．则a（a-2b）+（b+1）（b-1）=a2-2ab+b2-1=（a-b）2-1=（a-b+1）（a-b-1）=（m+n-mn+1）（m+n-mn-1），得证．
（☆☆）【27.3.2】
求证：（y+z-2x）3+（z+x-2y）3+（x+y-2z）3
=3（y+z-2x）（z+x-2y）（x+y-2z）.
【解析】
由于等式两边括号中代数式的一致性，令a=y+z-2x，b=z+x-2y，c=x+y-2z，由于a+b+c=y+z-2x+z+x-2y+x+y-2z=0，故可得a3+b3+c3-3abc=0，即得证．
【备注】
a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-bc-ac），若a+b+c=0，则有a3+b3+c3-3abc=0.
（☆☆☆）【27.3.3】
已知1 989x2=1 991y2=1 993z2，x＞0，y＞0，z＞0，且
，求证：
.
【解析】
令1 989x2=1 991y2=1 993z3=k（k＞0），则
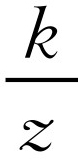.由于
，故
，由于
，故
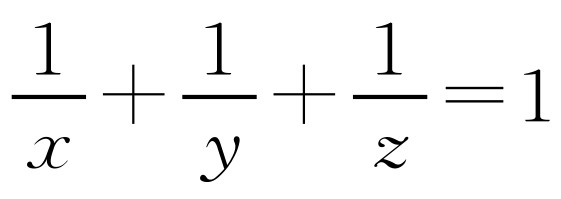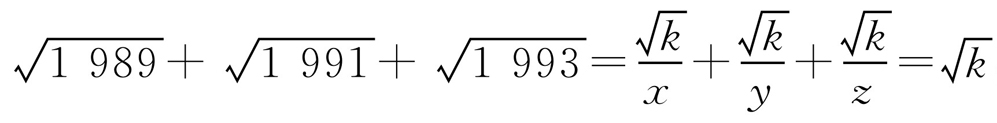，故得证．
（☆☆）【27.3.4】
是否存在常数C，使得不等式
对任意正数x，y恒成立？
【解析】
设2x+y=3m，x+2y=3n
得x=2m-n，y=2n-m
所以，存在常数C，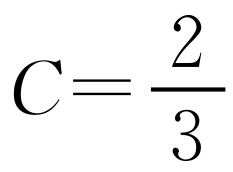
.
【备注】
本题中运用到了公式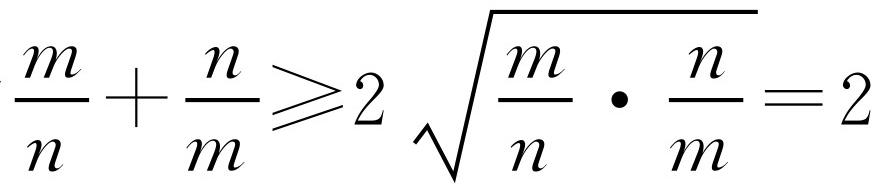
.
（☆☆☆）【巩固练习4】
求证：51 995-1能分解成三个整除之积，且每一个因数都大于5100.
在线客服
共有条评论 网友评论