试题4（2008年上半年试题66～67）
图21-4标明了六个城市（A～F）之间的公路（每条公路旁标注了其长度公里数）。为将部分公路改造成高速公路，使各个城市之间均可通过高速公路通达，至少要改造总计 （66） 公里的公路，这种总公里数最少的改造方案共有 （67） 个。
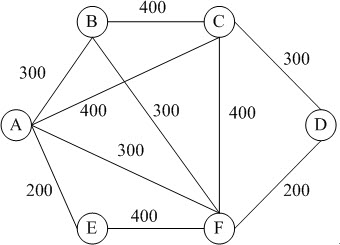
图21-4 高速公路图
（66）A．1000
B．1300
C．1600
D．2000
（67）A．1
B．2
C．3
D．4
试题4分析
这是一道求图的最小生成树问题，我们使用克鲁斯卡尔算法来解答。
设T的初始状态只有n个顶点而无边的森林T＝（V，￠），按边长递增的顺序选择E中的n－1条安全边（u，v）并加入T，生成最小生成树。所谓安全边是指两个端点分别是森林T里两棵树中的顶点的边。
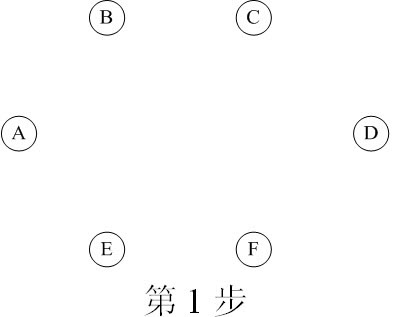
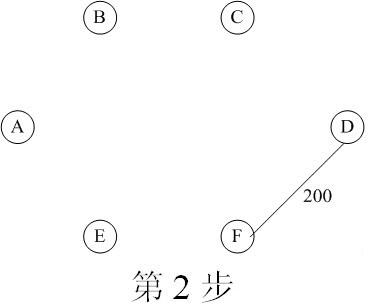
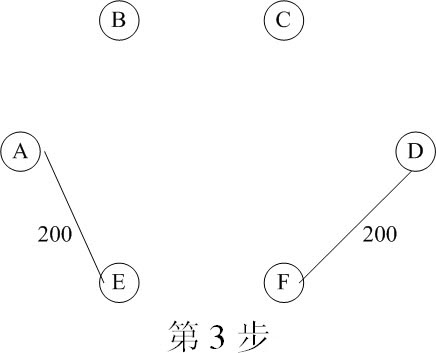
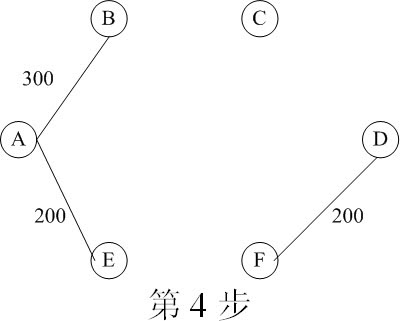
图21-5 求最小生成树的过程
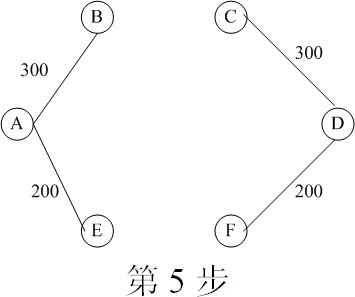
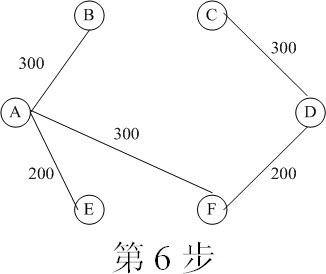
图21-5 求最小生成树的过程（续）
到了第5步，就有了多种选择，即可以选择AF，也可以选择BF，因为其路程都是300。我们给出的第6步是选择AF的结果。还有一种结果，就是在第4步时，不是选择AB，而是选择AF或者BF，则结果如图21-6所示。
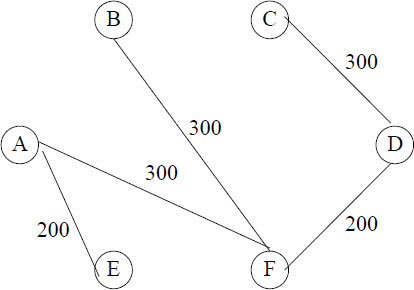
图21-6 另外一个结果
从第6步的结果可以计算出，至少要改造的公路长度为200×2＋300×3＝1300公里。
试题4答案
（66）B
（67）C
在线客服
共有条评论 网友评论